Вычисление арифметических выражений

5 марта 2023

Тэги: Java, maven, алгоритмы, головоломки, руководство.

Содержание

Лексический анализ
Обратная польская нотация
Алгоритм Дейкстры
Стековая машина
Соединяем всё воедино
Возможные улучшения

Давайте разберёмся, как можно вычислять арифметические выражения. Предположим, на вход нам поступает строка текста, которая содержит корректное арифметическое выражение.

" 20 * (10 - 5) "

Это выражение состоит из пробелов, чисел, скобок и знаков, обозначающих основные математические действия (плюс, минус, умножить, разделить). Нам нужно разобрать это выражение на отдельные элементы, а затем вычислить результат с учётом приоритетов математических операций. Например, умножение и деление должно выполняться раньше, чем сложение и вычитание. А часть выражения, заключённая в скобки, имеет приоритет над другими частями.

Обработку такого выражения можно разделить на три основных этапа:

Разбиение строки на отдельные части
Обработка этих частей с учётом математических операций
Само вычисление

Разберём каждую из этих частей подробнее.

Лексический анализ

Символы, сгруппированные по некоторому признаку, называются токеном. Лексический анализ или токенизация – процесс разбиения входной строки на отдельные токены. В нашем случае каждое число – это отдельный токен. Также токенами являются открывающая скобка, закрывающая и знаки математических операций. Пробелы тоже являются токенами, но на вычисление они никак не влияют, поэтому мы их будем пропускать.

Наличие или отсутствие пробелов никак не должно влиять на корректность разбиения на токены. Если вместе с числом слитно написана скобка или знак плюс, мы должны на выходе всё равно получить два токена.

Такой парсинг можно было бы реализовать и вручную по следующему алгоритму. Проходимся по каждому символу строки и проверяем его:

Если это пробел – ничего не делаем
Если текущий символ имеет тот же тип, что и предыдущий, то прибавляем его к существующему токену.
Если текущий символ имеет другой тип – начинаем «набирать» новый токен.

Однако писать такой код утомительно и можно легко ошибиться. Благо в Java есть стандартный класс для этого – StringTokenizer. Он разбивает исходную строку на подстроки по указанным разделителям и далее мы можем пройтись по ним в цикле.

Давайте создадим класс Lexer и сразу добавим в него константу с разделителями в виде строки:

public class Lexer {
private static final String DELIMITERS = " +-*/()";
}

Обратите внимание, что среди разделителей присутствует пробел.

Теперь давайте создадим перечисление TokenType, представляющее тип токена:

public enum TokenType {
    BINARY_OPERATION,
    NUMBER,
    OPEN_BRACKET,
    CLOSE_BRACKET
}

Как видите, токен может быть числом, открывающей скобкой, закрывающей, а также бинарной операцией. Под бинарной операцией здесь понимается любая математическая операция с двумя аргументами.

Сам токен представим в виде интерфейса:

public interface Token {
TokenType type();
}

Его реализуют несколько record-классов, по одному на каждый тип. В каждом таком классе может быть свой набор дополнительных полей.

NumberToken – представляет собой число и содержит его значение:

public record NumberToken(
        Integer value
) implements Token {
    @Override
    public TokenType type() {
        return TokenType.NUMBER;
    }
}

BinaryOperationToken – токен бинарной операции:

public record BinaryOperationToken(
        OperationType operationType
) implements Token {
    @Override
    public TokenType type() {
        return TokenType.BINARY_OPERATION;
    }
}

Он содержит поле OperationType, которое также является перечислением:

public enum OperationType {
    PLUS,
    MINUS,
    MULTIPLY,
    DIVIDE,
}

Для скобок создадим ещё одну реализацию интерфейса Token:

public record OtherToken(TokenType type) implements Token {
}

Теперь вернёмся к лексеру и добавим в него метод getTokens():

public List<Token> getTokens(String source) {
    StringTokenizer tokenizer = new StringTokenizer(source, DELIMITERS, true);
    List<Token> tokens = new ArrayList<>();
    // ...

Конструктор класса StringTokenizer принимает на вход исходную строку, разделители и флаг, указывающий на то, что разделители также нужно вернуть как отдельные токены. Это такой небольшой лайфхак, т.к. мы не должны потерять скобки и математические знаки.

Далее в цикле while с помощью методов hasMoreTokens() и nextToken() проходимся по каждому токену:

while (tokenizer.hasMoreTokens()) {
    String token = tokenizer.nextToken();
    if (token.isBlank()) {
        continue;
    } else if (isNumber(token)) {
        tokens.add(new NumberToken(Integer.parseInt(token)));
        continue;
    }

Если токен содержит пробел – пропускаем его.

Далее пытаемся проверить, не является ли токен числом? Если является, то создаём NumberToken и преобразуем строку токена в число. Саму проверку на принадлежность токена к числу выполняем тривиально:

private boolean isNumber(String token) {
    for (int i = 0; i < token.length(); i++) {
        if (!Character.isDigit(token.charAt(i))) {
            return false;
        }
    }
    return true;
}

Проходимся по каждому символу токена и вызываем для него метод Character.isDigit(). Если он вернёт false – сразу говорим, что это НЕ число.

Если же токен не пробел и не число, значит, по условию задачи, он является математической операцией или скобкой. Создаём соответствующий токен:

tokens.add(
        switch (token) {
            case "+" -> new BinaryOperationToken(OperationType.PLUS);
            case "-" -> new BinaryOperationToken(OperationType.MINUS);
            case "*" -> new BinaryOperationToken(OperationType.MULTIPLY);
            case "/" -> new BinaryOperationToken(OperationType.DIVIDE);
            case "(" -> new OtherToken(TokenType.OPEN_BRACKET);
            case ")" -> new OtherToken(TokenType.CLOSE_BRACKET);
            default -> throw new RuntimeException("Unexpected token: " + token);
        }
);

В итоге в списке tokens у нас окажутся все интересующие нас подстроки, уже имеющие соответствующий тип. И среди них гарантированно нет пробелов.

Обратная польская нотация

После лексического анализа приступаем к парсингу. Здесь нам предстоит учесть все правила математики и «перетасовать» наши токены так, чтобы в дальнейшем их было легко вычислить.

По большому счёту для парсинга арифметических выражений есть два способа: абстрактное синтаксическое дерево и обратная польская нотация. Будем использовать последнюю, т.к. она проще в реализации.

Польская нотация (прямая) – это форма записи арифметических выражений, которую придумал польский логик Ян Лукасевич. В ней сначала записывается математическое действие, а затем два аргумента для неё:

// польская нотация для 40 / 20
/ 40 20
// (5 − 6) * 7
* − 5 6 7

Интересной особенностью польской нотации является то, что в ней не требуются скобки (если все операторы бинарные).

Существует также обратная польская нотация, которую разработал Чарльз Хэмблин на основе «прямой» польской нотации. В ней сначала идут аргументы (числа), а затем действие над ними:

// обратная польская нотация для 40 / 20
/ 20 40
// (5 − 6) * 7
5 6 - 7 *

Обратите внимание, что в такой записи сначала идёт правый аргумент (делитель), а затем левый (делимое). Так уж получилось, что именно обратная польская нотация идеально подходит для вычислений на стеке благодаря простоте реализации.

Стек реализует принцип LIFO («последним пришёл – первым вышел»). Ближайшая аналогия – это стопка книг. Подробнее про стек можно почитать в статье Коллекции: очередь и стек.

Алгоритм Дейкстры

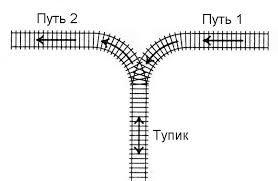
Теперь реализуем алгоритм, который будет конвертировать набор токенов из привычной нам записи в обратную польскую нотацию. Этот алгоритм разработал Эдсгер Дейкстра. Он назвал его «алгоритм сортировочной станции» за сходство алгоритма с процессом сортировки вагонов на железной дороге с использованием третьего пути.

Создадим метод convertToPostfix() и сразу заведём список токенов для обратной польской записи и стек для математических операций:

public List<Token> convertToPostfix(List<Token> source) {
List<Token> postfixExpression = new ArrayList<>();
Deque<Token> operationStack = new LinkedList<>();

Затем проходимся по каждому токену в исходной записи и проверяем его тип. Если это число – сразу добавляем в результат:

for (Token token : source) {
switch (token.type()) {
case NUMBER -> postfixExpression.add(token);

Если это открывающая скобка – добавляем её в стек операций:

case OPEN_BRACKET -> operationStack.push(token);

Если закрывающая скобка – извлекаем из стека все операции и добавляем их в результат, пока не дойдём до открывающей скобки. Затем просто удаляем открывающую скобку из стека:

case CLOSE_BRACKET -> {
    while (!operationStack.isEmpty() && operationStack.peek().type() != TokenType.OPEN_BRACKET) {
        postfixExpression.add(operationStack.pop());
    }
    operationStack.pop(); // открывающая скобка
}

Если же перед нами бинарная операция – извлекаем из стека все операции, у которых более высокий приоритет. Затем заносим текущую операцию в стек:

case BINARY_OPERATION -> {
    while (!operationStack.isEmpty() && getPriority(operationStack.peek()) >= getPriority(token)) {
        postfixExpression.add(operationStack.pop());
    }
    operationStack.push(token);
}

Вспомогательный метод getPriority() выглядит так:

private int getPriority(Token token) {
    if (token instanceof BinaryOperationToken operation) {
        return switch (operation.operationType()) {
            case PLUS, MINUS -> 1;
            case MULTIPLY, DIVIDE -> 2;
        };
    }
    return 0; // для открывающей скобки
}

Как видите, умножение и деление имеют более высокий приоритет, чем сложение и вычитание. У открывающей скобки самый низкий приоритет.

После выхода из цикла добавляем к результату всё, что осталось в стеке:

for (Token token : source) {
// case NUMBER, case OPEN_BRACKET ...
}
while (!operationStack.isEmpty()) {
postfixExpression.add(operationStack.pop());
}
return postfixExpression;

Теперь нам осталось взять наше выражение в обратной польской нотации и вычислить его на стековой машине.

Стековая машина

Как нетрудно догадаться, стековая машина производит вычисления на стеке значений. Она извлекает сначала один аргумент (правый), затем второй (левый), а затем выполняет над ними указанную операцию и заносит результат на вершину стека. Если обратная польская нотация корректна, то после завершения её обработки в стеке будет ровно 1 элемент, который и является результатом вычисления исходного арифметического выражения.

Создадим класс StackMachine и метод evaluate(). В нём создадим стек значений valueStack. Потом последовательно проходимся по токенам в обратной польской нотации. Если токен число – помещаем его на вершину стека.

public int evaluate(List<Token> postfixExpression) {
    Deque<Integer> valueStack = new LinkedList<>();
    for (Token token : postfixExpression) {
        if (token instanceof NumberToken number) {
            valueStack.push(number.value());
        }

Иначе если это бинарная операция, то извлекаем из стека два аргумента для неё: сначала правый, затем левый. Обратите внимание, что других типов токенов, кроме числа и операций здесь уже не будет.

else if (token instanceof BinaryOperationToken operation) {
int right = valueStack.pop();
int left = valueStack.pop();

Ну а далее выполняем действие, соответствующее типу операции и помещаем результат на вершину стека. При делении важно проверить правый аргумент (делитель), чтобы он не был равен нулю.

int result = switch (operation.operationType()) {
    case PLUS -> left + right;
    case MINUS -> left - right;
    case MULTIPLY -> left * right;
    case DIVIDE -> {
        if (right == 0) {
            throw new RuntimeException("Divide by zero!");
        }
        yield left / right;
    }
};
valueStack.push(result);

После выхода из цикла извлекаем единственный оставшийся элемент из стека – это и есть результат наших вычислений:

for (Token token : postfixExpression) {
// проверка типа токена и вычисления
}
return valueStack.pop();

Как видите, обратная польская нотация позволяет довольно легко вычислять арифметические выражения.

Соединяем всё воедино

Теперь вызовем последовательно лексер, конвертер и стековую машину, чтобы обработать исходное выражение целиком:

public int calculate(String expression) {
    List<Token> tokens = lexer.getTokens(expression);
    List<Token> postfixExpression = converter.convertToPostfix(tokens);
    int result = stackMachine.evaluate(postfixExpression);
    System.out.println(result);
    return result;
}

Теперь протестируем нашу реализацию:

Calculator calculator = new Calculator();
calculator.calculate(" 12*5 - 36 / 3"); // 48
calculator.calculate("12 + 50 / 5 - 3 "); // 19
calculator.calculate("20 * ( 45 + 5 ) / 10"); // 100
calculator.calculate(String.valueOf(Integer.MAX_VALUE)); // 2147483647

Рассмотренная в данной статье реализация калькулятора доступна на github.

Возможные улучшения

Наш калькулятор на текущий момент может обрабатывать только целые числа, представленные типом int. Если передать более «длинное» число, то при парсинге будет ошибка. Также хотелось бы обрабатывать десятичные дроби. Всё это довольно легко сделать, если заменить int на BigDecimal, а также доработать метод isNumber() в лексере, чтобы он допускал наличие десятичной точки в числе. При делении BigDecimal в стековой машине нужно учесть некоторые особенности округления, о которых я писал в статье Советы по работе с BigDecimal в Java.

Ну а дальше если к этому калькулятору добавить поддержку переменных, функций и управляющие конструкции (хотя бы if, else и while), то вы получите простейший интерпретатор языка программирования.

Облако тэгов

Kotlin, Java, Spring, Spring Boot, Spring Data, SQL, PostgreSQL, Oracle, Linux, Hibernate, Collections, Stream API, многопоточность, файлы, Nginx, Apache, maven, gradle, JUnit, YouTube, новости, руководство, ООП, алгоритмы, головоломки, rest, GraphQL, Excel, XML, json, yaml.