Алгоритм поиска чисел Фибоначчи

15 ноября 2024

Тэги: Java, Kotlin, алгоритмы, головоломки.

Содержание

Немного теории
Простая реализация на Java
Поддержка больших чисел
Рекурсивный вариант
Улучшенный рекурсивный вариант с массивом
Улучшенный рекурсивный вариант без массива
Пример на Kotlin
Итоги

Немного теории

На собеседованиях по алгоритмам любят давать такую задачку, как нахождение чисел из последовательности Фибоначчи. Эта числовая последовательность названа в честь Леонардо Пизанского – известного математика Средневековья.

Сама последовательность довольно проста. Она состоит из целых положительных чисел, где каждый следующий элемент равен сумме двух предыдущих. Например, 2 = 1 + 1, 3 = 2 + 1, 5 = 3 + 2.

Последовательность начинается с 0 и 1:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 ...

Иногда в этой последовательности принято пропускать 0 и начинать её с двух единиц, однако официально она начинается именно с 0.

Эта последовательность описывает правило «золотого сечения», когда мы делим нечто целое на две неравные части, где целая часть так же пропорциональна бОльшей, как и бОльшая к меньшей.

Считается, что это правило также часто встречается в природе. Например, в спиралях раковины моллюска или в спирали Млечного Пути.

Простая реализация на Java

Давайте напишем метод, который будет возвращать число Фибоначчи по его индексу в этой последовательности. Числа в последовательности растут очень быстро, поэтому значения будем хранить в типе long.

public long getFibonacciByIndex(int index) {
    if (index == 0) {
        return 0; // первый элемент последовательности
    }
    if (index < 0 || index > 92) {
        // при индексе 93 происходит переполнение типа long
        throw new IndexOutOfBoundsException(index);
    }
    long n0 = 0L;
    long n1 = 1L;
    for (int i = 2; i <= index; i++) {
        long n2 = n0 + n1;
        n0 = n1;
        n1 = n2;
    }
    return n1;
}

Алгоритм тут довольно простой: заводим первые два числа последовательности как n0 и n1. Затем в цикле, начиная с индекса 2, вычисляем новое значение как их сумму. Это новое значение становится n1, а то, что было n1 – становится n0. По достижении необходимого индекса выходим из цикла и возвращаем результат.

Обратите внимание на обработку пограничных случаев. Если индекс равен 0 – сразу возвращаем первый элемент последовательности, т.е. 0. Отрицательный индекс недопустим – кидаем стандартное исключение IndexOutOfBoundsException.

Также кидаем исключение, если индекс больше чем 92 – тут происходит переполнение типа long. При переполнении Java ошибку не кидает, но число при этом становится некорректным (например, отрицательным). Это связано со сдвигом и потерей части разрядов в двоичном представлении числа.

Теперь можем вызвать наш метод и посмотреть число Фибоначчи с индексом, например, 42.

public class Fibonacci {
    public static void main(String[] args) {
        var fibonacci = new Fibonacci();
        System.out.println(fibonacci.getFibonacciByIndex(42)); // выведет 267914296
    }
    // ...
}

Данная реализация работает довольно шустро и её единственный недостаток – это поддержка только первых 92 членов последовательности. Но что, если мы хотим вычислить элемент с индексом 100, 1000 или даже 1 000 000 ?

Поддержка больших чисел

На помощь нам придёт класс BigInteger. Он довольно громоздкий с точки зрения скорости вычисления и с точки зрения написания кода, но при этом поддерживает сколь угодно большие числа. Поэтому заменим long на BigInteger. Желаемый номер элемента также будем передавать в метод как BigInteger.

public BigInteger getFibonacciByIndexInfinite(BigInteger index) {
    if (index.compareTo(BigInteger.ZERO) == 0) {
        return BigInteger.ZERO;
    }
    if (index.compareTo(BigInteger.ZERO) < 0) {
        throw new IndexOutOfBoundsException(index.toString());
    }
    var n0 = BigInteger.ZERO;
    var n1 = BigInteger.ONE;
    for (var i = BigInteger.TWO; i.compareTo(index) <= 0; i = i.add(BigInteger.ONE)) {
        var n2 = n0.add(n1);
        n0 = n1;
        n1 = n2;
    }
    return n1;
}

Тут мы уже не можем использовать числа типа 0 и 1. Вместо этого пишем константы BigInteger.ZERO и BigInteger.ONE. Сравнение чисел также усложняется – используем метод compareTo(). Для сложения вместо плюса пишем метод add(). Поскольку BigInteger поддерживает очень большие числа, то проверку на максимальный индекс убираем.

Теперь мы можем найти элемент с порядковым номером 1 000 000. Обратите внимание, что BigInteger можно инициализировать через текстовое представление числа.

System.out.println(fibonacci.getFibonacciByIndexInfinite(new BigInteger("1000000")));
// найденное число состоит из 208988 цифр!

Найденный результат представляет собой столь большое число, что оно не помещается на экран консоли! Даже на 20 экранов... Однако и это число на моём ноуте было вычислено всего-то за 15 секунд.

Согласитесь, вряд ли может потребоваться вычислять столь большие значения, поэтому можно считать, что даже с BigInteger алгоритм всё равно работает шустро.

Рекурсивный вариант

Алгоритм поиска чисел Фибоначчи также можно реализовать с помощью рекурсии, т.е. когда метод будет вызывать сам себя.

public long getFibonacciByIndexRecursive(int n) {
    if (n == 0 || n == 1) {
        return n;
    }
    return getFibonacciByIndexRecursive(n - 1) + getFibonacciByIndexRecursive(n - 2);
}

В любом методе с рекурсией обязательно должны быть условия остановки, проверяющие пограничные значения. Здесь мы проверяем индекс, переданный в параметре. Если он 0 или 1 – тут же возвращаем число. Иначе возвращаем результат, как вызов этого же метода с параметрами n – 1 и n – 2 с последующим их суммированием.

Как видите, рекурсивный алгоритм довольно компактен. Но у него есть два недостатка.

Во-первых, для рекурсии активно используется стек вызова методов. Вы можете довольно легко исчерпать его и получить StackOverflowError, запросив какой-нибудь большой индекс.

Схема рекурсивного вычисления последовательности Фибоначчи

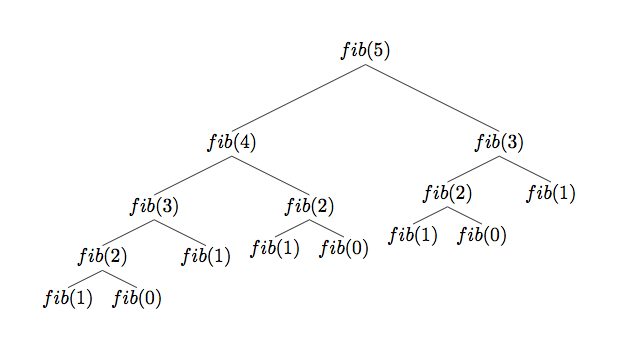
Во-вторых, и это более критично, время вычисления каждого следующего числа в два раза больше предыдущего. Для малых индексов это не так заметно, но где-то в районе 45-го числа последовательности задержка уже даёт о себе знать. Дело в том, что мы вычисляем все предыдущие значения на каждом уровне рекурсии, несмотря на то, что уже вычисляли их ранее.

Улучшенный рекурсивный вариант с массивом

Эту проблему можно решить кешированием уже вычисленных значений. Доработаем предыдущий метод, добавив туда второй параметр memo, представляющий собой массив целых чисел, допускающих null-значения, т.е. ссылочный тип Long.

public long getFibonacciByIndexRecursiveWithArray(int n, Long[] memo) {
    if (n == 0 || n == 1) {
        memo[n] = (long) n;
        return n;
    }
    if (memo[n] == null) {
        long res = getFibonacciByIndexRecursiveWithArray(n - 2, memo) + getFibonacciByIndexRecursiveWithArray(n - 1, memo);
        memo[n] = res;
    }
    return memo[n];
}

При вызове метода передаём пустой массив с количеством ячеек, равным количеству чисел в последовательности + 1. Вместо массива можно также использовать обычный List.

getFibonacciByIndexRecursiveWithArray(index, new Long[index + 1]);

Теперь мы каждый раз перед вычислением проверяем, нет ли уже такого значения в кеше. Если значение уже вычислено, то под соответствующим индексом в memo будет число, а не null. Это даёт значительное ускорение работы метода.

Улучшенный рекурсивный вариант без массива

В оптимизации рекурсивного варианта можно пойти ещё дальше. Одним из недостатков приведённого выше варианта является дополнительный расход памяти для массива memo, причём пропорциональный количеству элементов. Использование массива было бы действительно необходимо, если бы вычисляли элементы в случайном порядке. Но так как мы их вычисляем всегда последовательно, это позволяет нам провести ещё одну оптимизацию.

Если мы вспомним, что каждое следующее число в последовательности является суммой двух предыдущих, то мы можем накапливать эту сумму, двигаясь от начальных элементов до элемента с нужным нам индексом. Также это позволит нам сократить количество рекурсивных вызовов в два раза.

public long getFibonacciByIndexRecursiveOptimized(int n) {
    if (n <= 1) {
        return n;
    }
    return getFibonacciByIndexRecursiveOptimized(n, 0, 1);
}

private long getFibonacciByIndexRecursiveOptimized(int n, long left, long right) {
    if (n < 2) {
        return right;
    }
    long sum = left + right;
    return getFibonacciByIndexRecursiveOptimized(n - 1, right, sum);
}

Основная идея, применённая в методе getFibonacciByIndexRecursiveOptimized() заключается в том, что мы передаём порядковый номер нужного нам элемента, а также правый и левый элементы. Изначально правый и левый элементы равны 0 и 1. На каждой итерации мы складываем правый и левый элементы. Эта сумма передаётся на следующую рекурсивную итерацию как новый правый элемент, а правый с предыдущей итерации становится левым для следующей. При этом каждый раз уменьшаем целевой индекс на 1. То есть значения элементов у нас возрастают, а индекс уменьшается до тех пор, пока не станет меньше 2-х. Когда это условие выполнится, правый элемент окажется искомым числом.

Благодаря такой реализации мы ускорили рекурсию и при этом не расходуем память.

Пример на Kotlin

В дополнение приведу вариант без рекурсии на Kotlin, чтобы продемонстрировать лаконичность его синтаксиса.

fun getFibonacciByIndexInfinite(index: BigInteger): BigInteger {
    if (index == BigInteger.ZERO) {
        return BigInteger.ZERO
    }
    if (index < BigInteger.ZERO) {
        throw IndexOutOfBoundsException(index.toString())
    }
    var n0 = BigInteger.ZERO
    var n1 = BigInteger.ONE
    var i = BigInteger.TWO
    while (i <= index) {
        val n2 = n0 + n1
        n0 = n1
        n1 = n2
        i++
    }
    return n1
}

Здесь всё ровно то же самое, только мы заменили цикл for на while. А также вернули обратно привычные нам операторы сравнения и инкремента. Теперь вызовем этот метод:

fun main() {
println(Fibonacci().getFibonacciByIndexInfinite(BigInteger("1000000")))
}

Время вычисления не увеличилось по сравнению с Java-версией, поскольку компилятор Kotlin вызывает те же самые compareTo() и add(), генерируя почти такой же байт-код.

Итоги

Мы рассмотрели несколько реализаций нахождения числа Фибоначчи по его индексу.

Наиболее простая реализация на Java использует примитивный тип long. Он работает быстро, но уже на 93-м элементе последовательности происходит переполнение.

Чтобы вычислять числа с бОльшим индексом, мы использовали класс BigInteger, который хоть и значительно медленнее примитива, но всё равно довольно шустро вычисляет огромные числа.

Также узнали про рекурсивный вариант реализации, который выглядит просто, но работает очень медленно для больших индексов последовательности.

Научились ускорять рекурсивный вариант путём добавления кеширования промежуточных результатов.

Наконец, мы рассмотрели реализацию на Kotlin. Благодаря лаконичному синтаксису метод выглядит менее громоздко и при этом не теряет в производительности.

P.S. Спасибо Диме Вдовину, который является автором telegram-канала Yet another backend digest, за комментарий о вычислительной сложности рекурсивного алгоритма.

P.P.S. Спасибо пользователю по имени Владимир, который в комментариях предложил вариант оптимизации рекурсивного алгоритма без использования массива.

См. также

Облако тэгов

Kotlin, Java, Spring, Spring Boot, Spring Data, SQL, PostgreSQL, Oracle, H2, Linux, Hibernate, Collections, Stream API, многопоточность, чат-боты, нейросети, файлы, devops, Docker, Nginx, Apache, maven, gradle, JUnit, YouTube, новости, руководство, ООП, алгоритмы, головоломки, rest, GraphQL, Excel, XML, json, yaml.