Алгоритм поиска суммы двух элементов в массиве

Содержание

1. Поиск суммы через вложенный цикл
2. Поиск суммы с помощью мапы
3. Поиск суммы на упорядоченном массиве
4. Выводы

На собеседованиях и на leetcode можно встретить такую алгоритмическую задачу. Дан неупорядоченный массив целых чисел. Нужно найти все пары чисел, сумма которых равна указанной. Числа в массиве могут быть как положительными, так и отрицательными. В качестве результата нужно вернуть порядковые индексы найденных элементов.

Например, если дан массив [2, 7, 11, 15] и целевая сумма равна 9, то правильным ответом будут индексы 0 и 1 (то есть первый и второй элементы массива), т.к. 2 + 7 = 9.

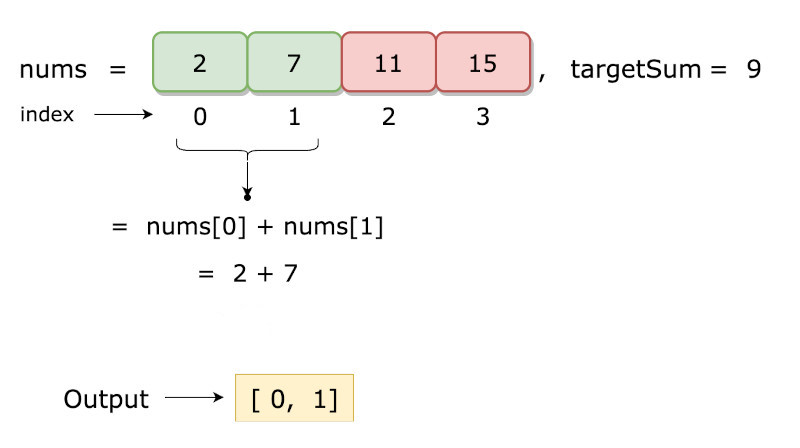
Рассмотрим несколько вариантов реализации этого алгоритма.

Поиск суммы через вложенный цикл

Самое простое решение – перебрать все возможные комбинации пар элементов и проверить их сумму. В этом нам поможет вложенный цикл.

Внешний цикл просто перебирает все элементы по порядку до предпоследнего элемента. И на каждой итерации внешнего цикла мы запускаем ещё один цикл от текущего элемента до конца массива. Внутри вложенного цикла проверяем сумму элементов с индексами i и j. Если сумма равна целевой – выводим пару индексов на экран. При этом также проверяем, что индексы не совпадают.

Проверим работу нашего метода на тестовых данных:

Как видим, метод работает корректно. Но давайте попробуем оценить его алгоритмическую сложность. Как только мы видим вложенный цикл, это сразу намекает на квадратичную сложность или O(n ^ 2). То есть время работы метода пропорционально квадрату от количества элементов исходного массива. Эта сложность далека от идеальной.

Поиск суммы с помощью мапы

Чтобы уменьшить алгоритмическую сложность, надо избавиться от вложенного цикла и сделать все проверки за один проход. Как этого добиться?

Давайте вспомним элементарную математику. Если перед нами «правильная» пара, то при вычитании из целевой суммы одного слагаемого мы должны получить второе слагаемое. Поэтому можно построить мапу, где ключом будет разница между целевой суммой и текущим элементом, а значением – индекс текущего элемента в массиве.

Теперь нам достаточно выполнить один проход по массиву, для каждого элемента проверяя наличие разницы между targetSum и текущим элементом в мапе. Если такой элемент найден, то один индекс – это индекс текущего элемента, а второй индекс – тот, который лежит в мапе. Если этой разницы в мапе не нашлось, то добавляем её в качестве ключа, а в качестве значения – текущий индекс i.

Обратите внимание, что для индекса j мы используем ссылочный Integer, а не примитивный int, т.к. если в мапе значение не найдено, она вернёт null. Преимуществом мапы является тот факт, что доступ по ключу происходит в среднем за константное время, т.е. за O(1). Индекс j, если он найден в мапе, будет заведомо меньше, чем индекс i, поэтому сначала выводим на экран j, потом i.

Алгоритмическая сложность данной реализации прямо пропорциональна количеству элементов, т.е. O(N). Такая сложность является вполне приемлемой.

Поиск суммы на упорядоченном массиве

Если известно, что массив заранее упорядочен, то задача поиска упрощается. Нам даже не потребуется дополнительная память.

Мы поставим индекс i в начало массива, индекс j – в конец массива, и в цикле while будем проверять на каждой итерации сумму элементов по этим индексам.

Если сумма окажется больше требуемой – сдвигаем влево индекс j, чтобы получить заведомо меньший элемент. Если сумма оказалась меньше целевой – сдвигаем вправо индекс i, чтобы получить бОльший элемент.

Если сумма равна целевой – пара найдена. Поэтому сдвигаем к центру массива оба индекса, чтобы перейти к поиску следующей пары.

Действия выполняются в цикле до тех пор, пока i меньше j.

Алгоритмическая сложность данной реализации также O(N).

Если бы мы искали не порядковые индексы, а сами элементы, то задачу поиска на неупорядоченном массиве можно было бы выполнить с помощью данного метода, предварительно отсортировав массив.

Выводы

За уменьшение алгоритмической сложности мы всегда вынуждены чем-то платить: либо дополнительными действиями, либо дополнительным расходом памяти. Но наиболее оптимальная сложность для неупорядоченного массива оказалась компромиссной: 1 цикл и 1 вспомогательная коллекция.

Существуют разные варианты задачи о поиске суммы двух элементов. Например, если требуется вывести только 1 пару индексов, то после её нахождения остальные элементы можно не проверять и сразу делать return после вывода элементов на экран.

Про какие ещё вариации поиска суммы вы хотели бы почитать? Пишите в комментариях.